Deep Neural Decision Forests

深度神经决策森林

xzhren@pku.edu.cn 任星彰

ICCV-2015 Best Paper / IJCAI-2016

微软剑桥研究院 / 卡内基梅隆大学 / 意大利布鲁诺凯斯勒研究中心

系列文章

• S. Schulter, P. Wohlhart, C. Leistner, A. Saffari, P. M. Roth, and H. Bischof.

Alternating decision forests. In (CVPR), 2013.

• Kontschieder P. Neural Decision Forests for Semantic Image Labelling. In(CVPR),

2014.

• Murthy V N, Singh V, Chen T, et al. Deep Decision Network for Multi-class Image

Classification. In(CVPR), 2016:2240-2248.

• Roy A, Todorovic S. Monocular Depth Estimation Using Neural Regression Forest.

In(CVPR), 2016:5506-5514.

• Ahmed K, Baig M H, Torresani L. Network of Experts for Large-Scale Image

Categorization. ECCV. 2016.

• Biau G, Scornet E, Welbl J. Neural Random Forests[J]. 2016.

• N. F, G. Hinton. Distilling a Neural Network Into a Soft Decision Tree. 2017.11.27

软决策树

• Distillation 蒸馏技术

• Soft Decision Tree 软决策树

NewYorkTimes：https://www.nytimes.com/2017/11/28/technology/artificial-intelligence-research-toronto.html

But Mr. Hinton believes his capsule networks can

eventually expand to a wider array of situations,

accelerating the progress of computer vision and things like

conversational computing. Capsule networks are an attempt to

mimic the brain’s network of neurons in a more complex and

structured way, and he explained that this added structure

could help other forms of artificial intelligence as well.

He certainly understands that many will be skeptical

of his technique. But Mr. Hinton also pointed out that five

years ago, many were skeptical of neural networks.

“History is going to repeat itself,” he said. “I think.”

• 随机路由决策树

• 决策树的BP算法

• 整体架构

• 实验效果

• 代码实现

• 结论与讨论

符号体系

• 样本集

• 标签集

• 决策节点集

• 叶子节点集

• 叶子节点 l 在标签集里的概率分布

• 决策节点n的决策函数，是参数

• 决策森林F，决策树T

随机路由决策树

• Routing：决策节点n的决策函数d

• 核心：确定性路由 -> 概率性路由

对于x到达叶子节点l4的路由函数µ

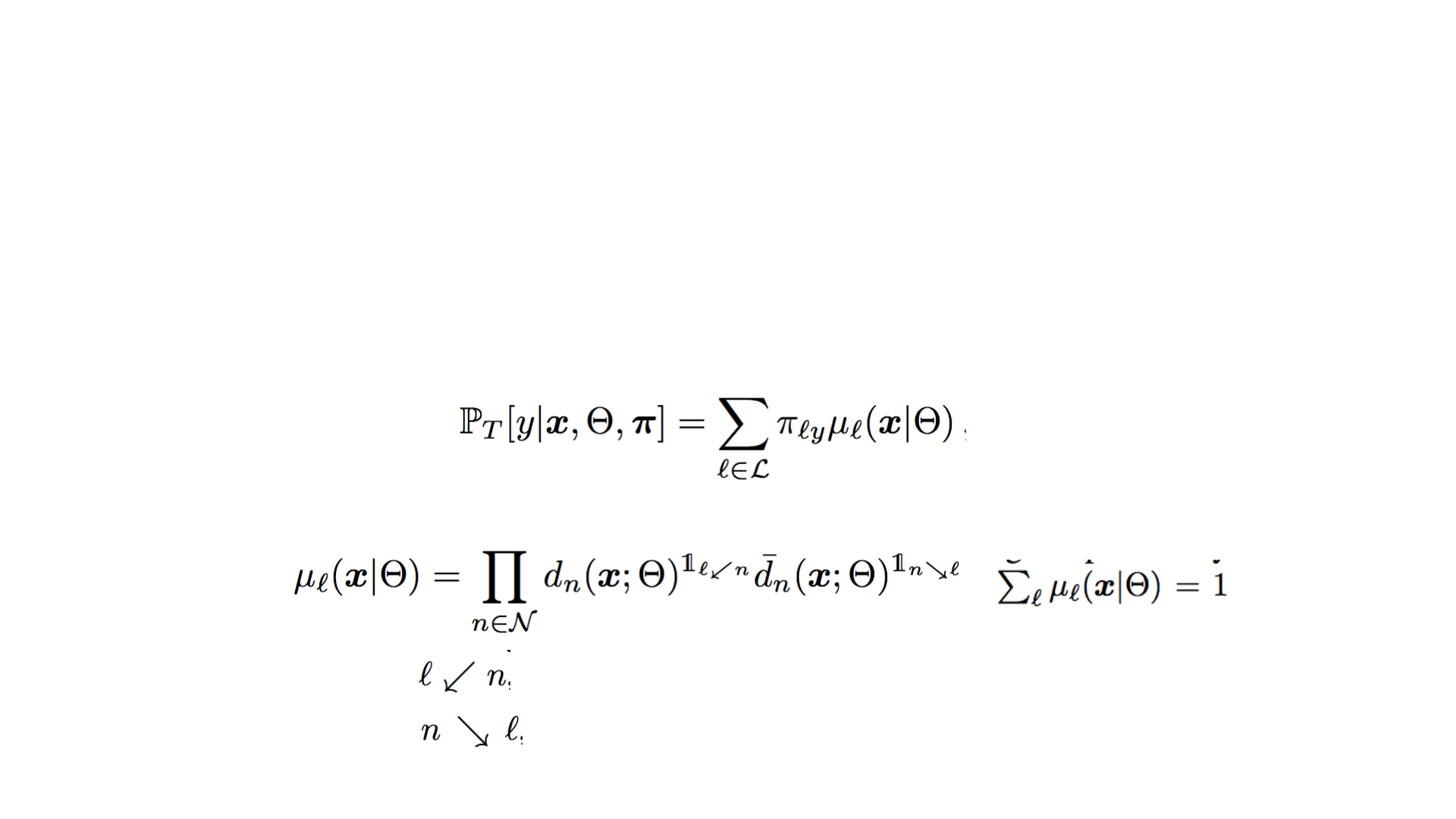
随机路由决策树

• Routing：决策节点n的决策函数d

• 核心：确定性路由 -> 概率性路由

01指示函数：当且仅当l是n的左子树为1

01指示函数：当且仅当l是n的右子树为1

决策树T对于x最终预测为y的概率

对于x到达叶子节点l的路由函数µ

随机路由决策树

• Routing：决策节点n的决策函数d

• 核心：确定性路由 -> 概率性路由

对于x决策节点n的决策函数

决策节点n的实值函数

决策森林F对于x预测为y的概率

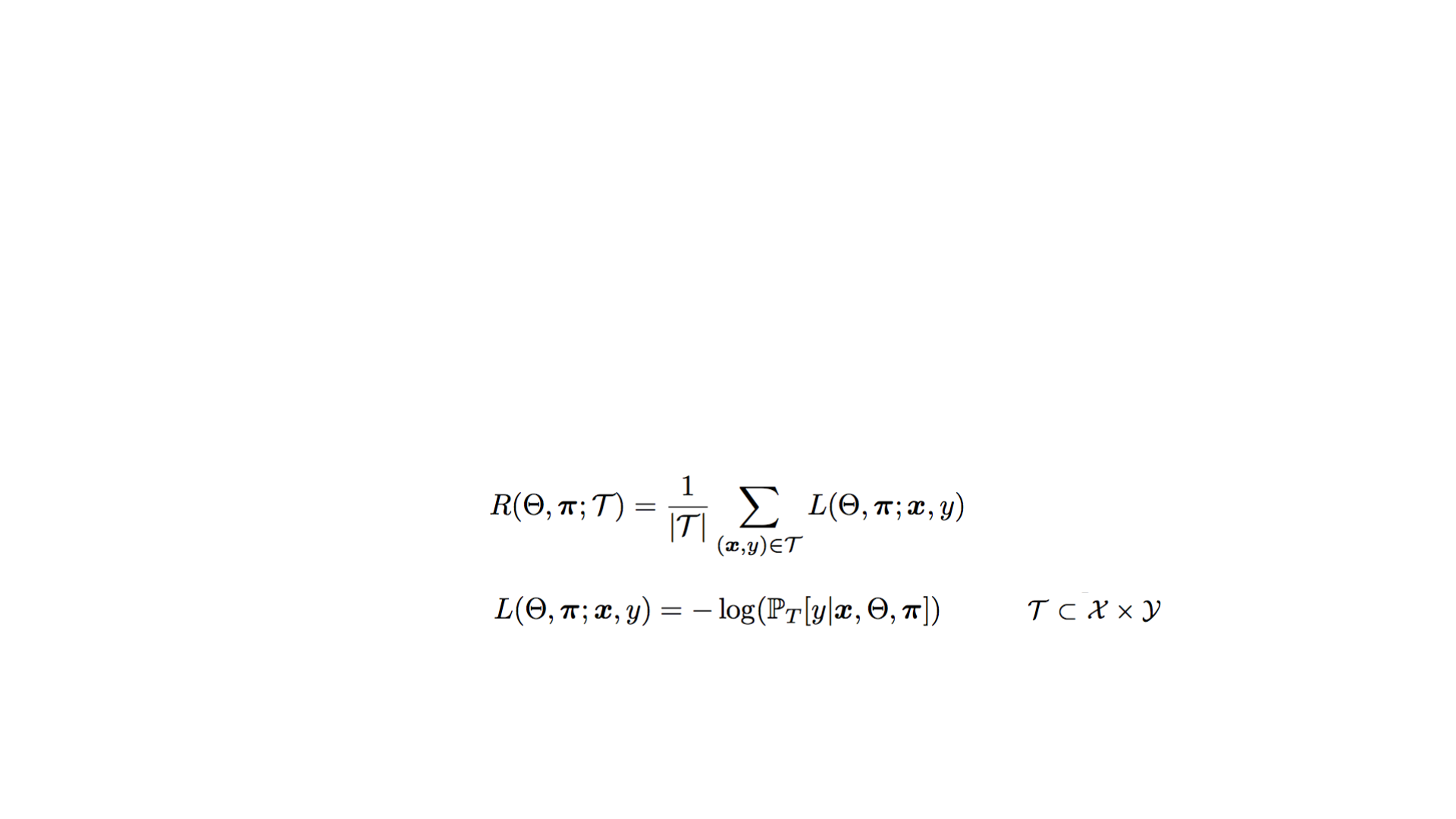
决策树的BP算法

• 两步优化策略

• 固定叶子节点分布更新决策树参数

• 固定决策树参数更新叶子节点分布

风险函数

log损失函数

决策树的BP算法

• 决策节点学习

• 学习方法：

• SGD

• RPROP

学习率

Mini Batch

m后所有的叶子节点

参数更新梯度

Resilient Back-Propagation

决策树的BP算法

• 叶子节点学习

• 学习方法：

• 线下学习

标准化因子

迭代策略

P.s. It is interesting to note that the update rule in (11) is step-size free and

it guarantees a strict decrease of the risk at each update until a fixed-point

is reached (see proof in supplementary material).

决策树的BP算法

• 森林学习

• 学习方法：

• dropout

we randomly select a tree in F for each mini-batch and then we

proceed as detailed in Subsection 3.1 for the SGD update.

each SGD update is potentially applied to a different network

topology, which is sampled according to a specific distribution.

updating individual trees instead of the entire forest reduces the

computational load during training.

策略：

优点1：

优点2：

决策树的BP算法

• 学习过程总结

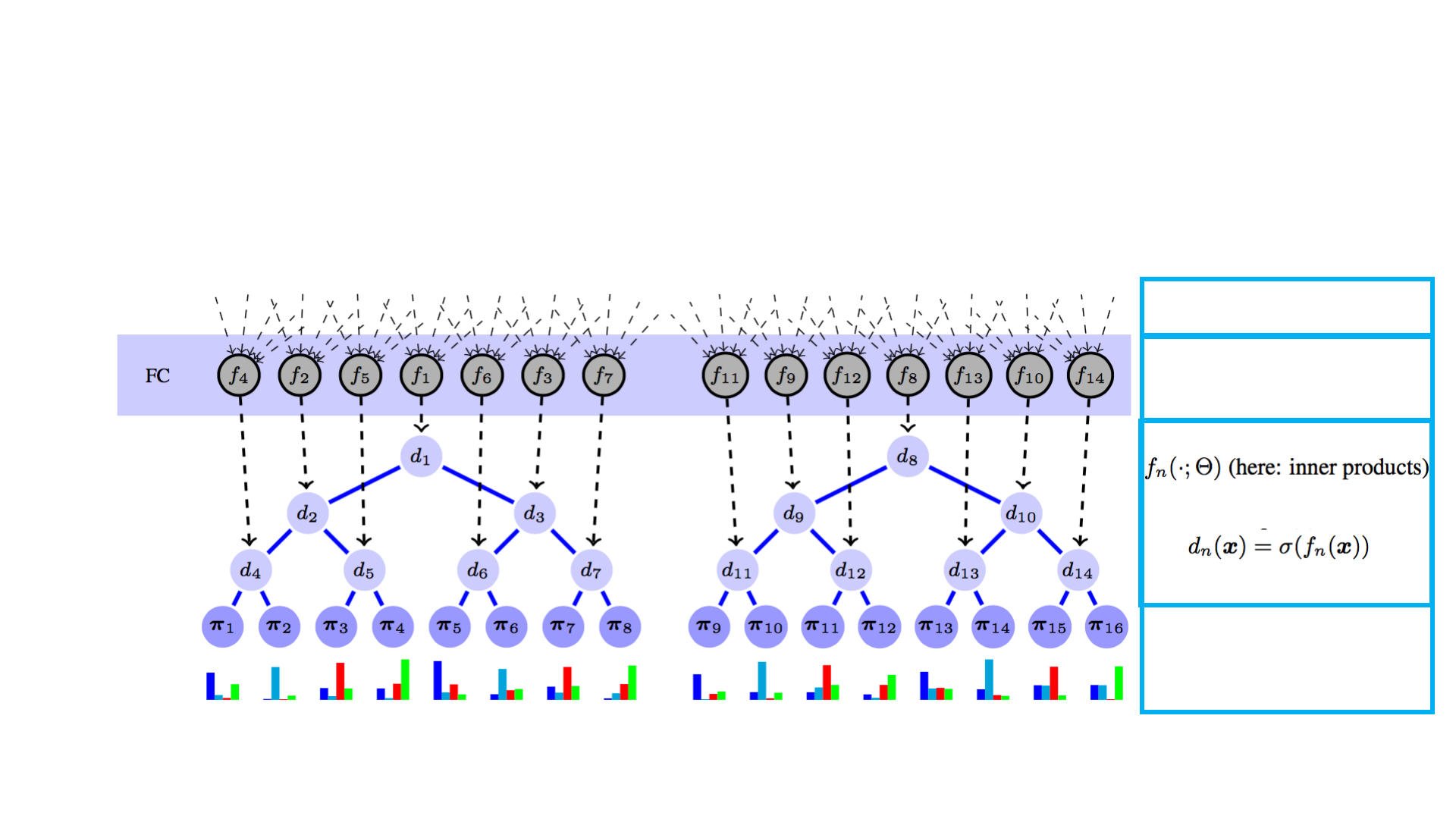
整体架构

• 决策过程

Deep CNN

FC block

routing (split) decisions

leaf nodes

probability distributions

整体架构

• 决策节点

• 迭代策略：

oblique forests

D. Heath, S. Kasif, and S. Salzberg. Induction of oblique decision trees.

Journal of Artificial Intelligence Research,

1.2(2):1–32, 1993.

20 iterations were

enough for all our

experiments

节点的实现

• 决策节点

• 路由函数

• 学习决策节点

• 学习预测节点

oblique forests

D. Heath, S. Kasif, and S. Salzberg. Induction of oblique decision trees.

Journal of Artificial Intelligence Research,

1.2(2):1–32, 1993.

迭代策略：20 iterations were enough for all our experiments

实验效果

• 对比实验 - 基础分类器对比

• sNDF：shallow neural decision forests 独立分类器

• ADF：alternating decision forests CVPR-2013

实验效果

• 对比实验 – 深度学习模型对比

• dNDF：deep neural decision forests 深度神经决策森林

• GoogleLeNet：

• GoogleLeNet*

• dNDF.NET：

MNIST：LeNet 0.9%，dNDF+LeNet 0.7%

ImageNet：GoogleLeNet 7.89%，dNDF.NET 6.38%

C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke,

and A. Rabinovich. Going deeper with convolutions. CoRR, abs/1409.4842, 2014.

replaced each Soft-max layer from GoogLeNet⋆ with a forest consisting of 10 trees

(each fixed to depth 15), resulting in a total number of 30 trees

GoogleLeNet

• Inception

dNDF.NET

实验效果

• 树节点评估

代码实现

• Input：-1 x 28*28*1

• L1：CNN/MaxPool/Dropout：-1 x 14*14*32

• L2： CNN/MaxPool/Dropout：-1 x 7*7*64

• L3： CNN/MaxPool/Dropout：-1 x 4*4*128

• FC / NDF：5 Tree，3 Depth

• Output：-1x10

代码实现

• # Load dataset

• # Initialize network weights

• # Define a fully differentiable deep-ndf

• # The routing probability computation

• # Define p(y|x)

• # Define cost and optimization method

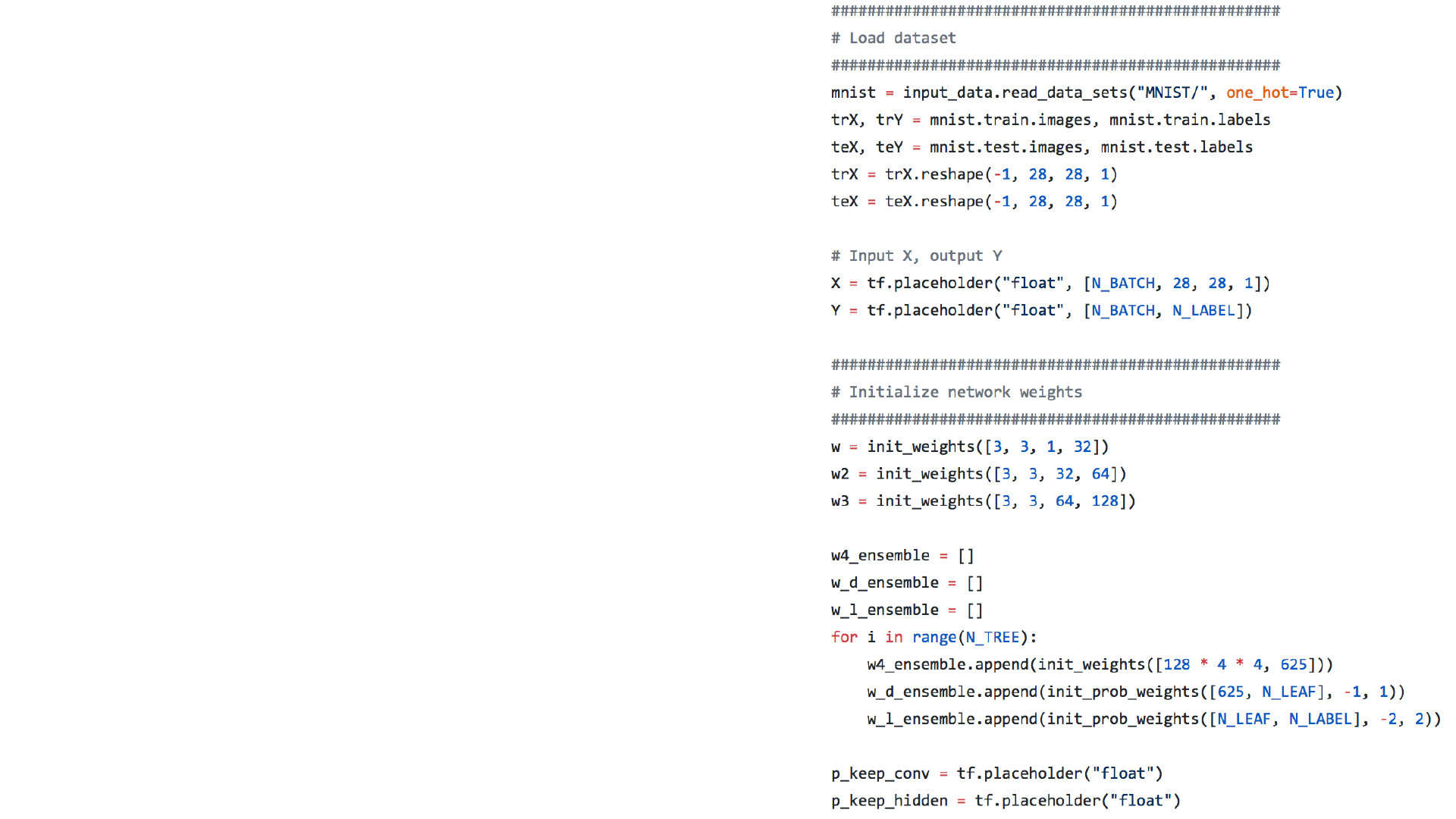
代码实现

• # Load dataset

• # Input X, output Y

• # Initialize network weights

• w1, w2, w3

• w4_ensemble, w_d_ensemble, w_l_ensem

• p_keep_conv, p_keep_hidden

代码实现

• Model

• 输入：

• X, w, w2, w3, w4_e, w_d_e, w_l_e,

p_keep_conv, p_keep_hidden

• 输出：

• decision_p_e:决策节点的路由概率

• leaf_p_e:叶子节点的概率分布

代码实现

• dNDF

• mu：路由概率

• flat_decision_p

• mu的初始值

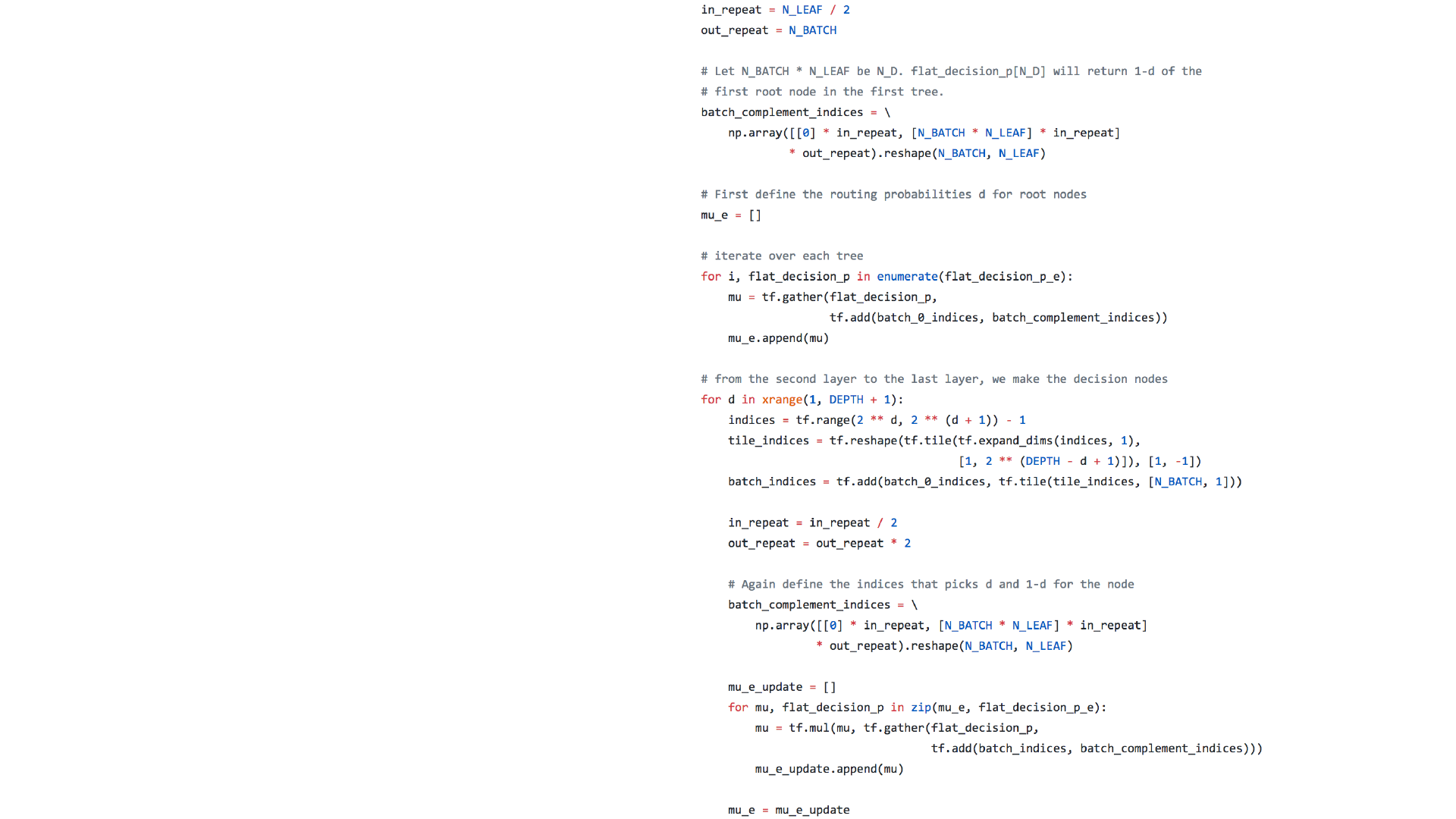
代码实现

• 概率路由计算

• 更新mu

mu = [d_0, d_0, d_0, d_0, 1-d_0, 1-d_0, 1-d_0, 1-d_0]

mu = mu * [d_1, d_1, 1-d_1, 1-d_1, d_2, d_2, 1-d_2, 1-d_2]

mu = mu * [d_3, 1-d_3, d_4, 1-d_4, d_5, 1-d_5, d_6, 1-d_6]

Tree indexing

1 2

3 4 5 6

代码实现

• 求p(y|x)

决策树T对于x最终预测为y的概率

代码实现

• 优化方法及过程

• 利用RMSP优化器

• 定义损失：

• 交叉熵损失函数

• 训练：

• RMSPoptimzer

• 测试：

• Accuracy

结论讨论

• 效果对比

CNN

Deep

-NDF

Decision Forest

Feature Learning

Yes

Divide

-and-conquer

Yes

Mutual Information Maximization

Yes

Ease of parallelization

Difficult

Easy

Gradient Descent

Yes

Convexity of loss

Convex

N/A

结论讨论

• 疑问：

• 决策树的路由顺序是如何确定的

• F函数的其他选择

• 改进：

• Forest的设计过于简单

• F函数的选择与讨论

• 结果可视化方面的工作

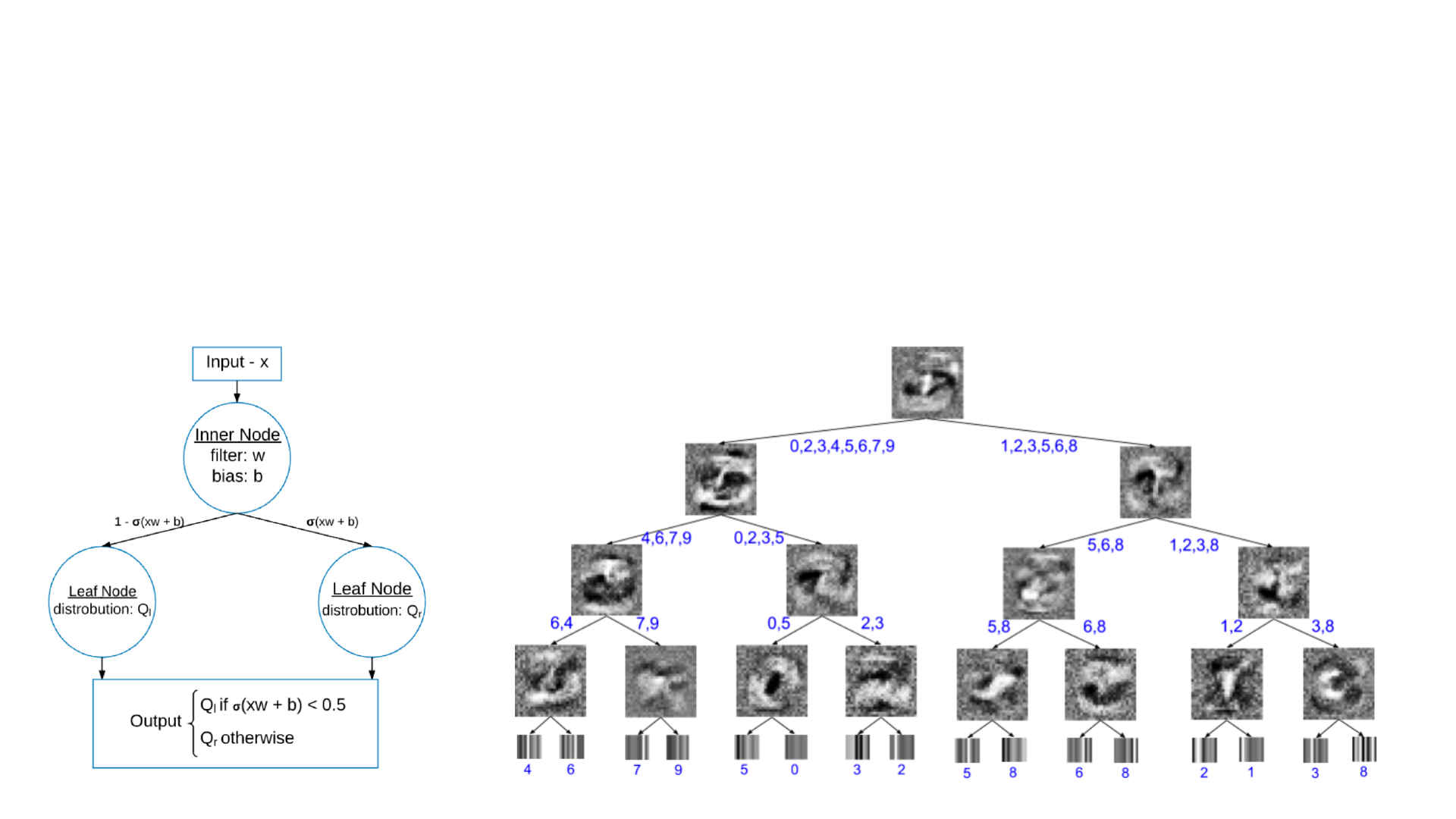
软决策树

• 作者在可泛化和可解释性之间取得了一个平衡

• 没有试图去了解深度神经网络如何做出决定，而是使用深度神经网络训练了

一个决策树，让这个决策树去模仿神经网络发现的输入输出函数